7月22日は「円周率の日」?
「円周率」について書いてみる。
他の多くの数字と異なり、「〜数」ではなく「〜率」という名前で呼ばれる。けれどもれっきとした数である。
小学生の頃にしれっと現れて以来、数学の授業では当たり前に登場するけれど、「3」や「3.14」や「π」などと姿を変える。
おかげで存在自体はよく知っているのに、名前や姿にぴんとこない、いまひとつ形を掴めないでいた。この数について考えてみる。
「円周率」とは何か
「『円周率』とは何か?」と聞かれたら、私はこう答える。
円の周りの長さを求めるための数(倍率)
「円周」を求めるための倍「率」、だから「円周率」。
わかったような、わからないような。
だから、自分を納得させるために図を書いた。
「円周率」の名前の由来
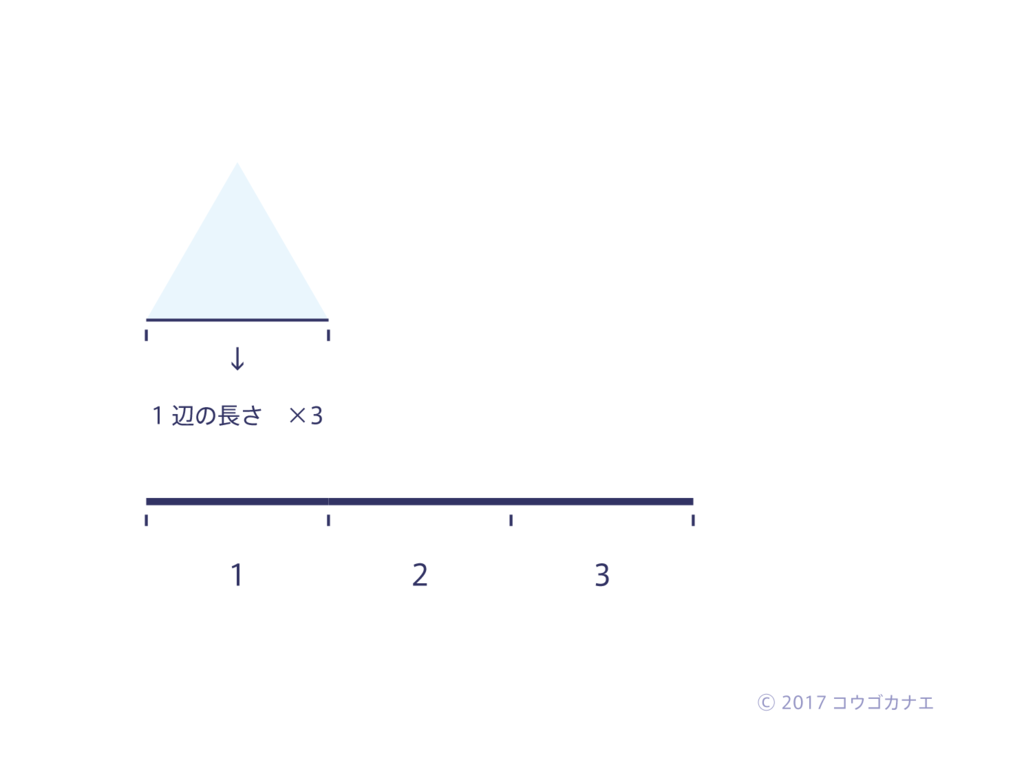
突然だが、正三角形について考える。
正三角形の1辺の長さを3倍にすると、正三角形の周りの長さが出る。
次に、正方形について考える。
正方形の1辺の長さを4倍にすると、正方形の周りの長さが出る。

最後に、円について考える。
円の直径を3.14倍にすると、円の周りの長さ(=円周)が出る。
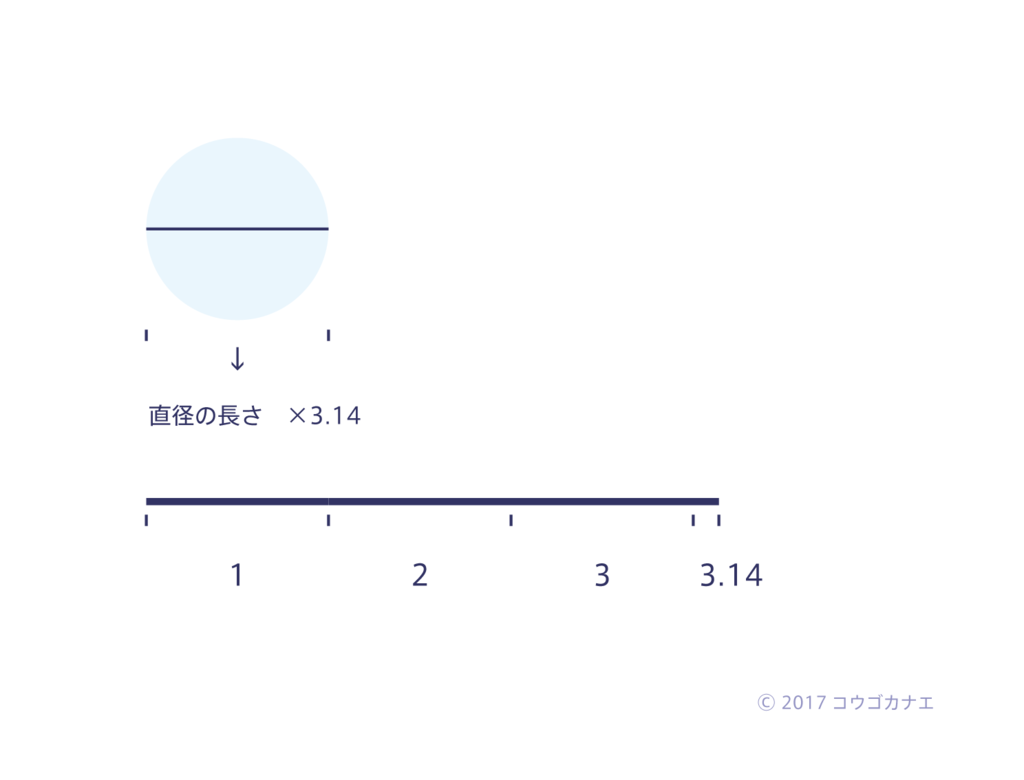
この3.14が円周率である。
つまり、「円の周りの長さを求めるための数」である。
そう考えるようにして、やっと納得できるようになった。
これを他のひとに説明する機会はまだない。ちなみに、便宜上3.14として記載したが3.14はあくまでも近似値である。
円周率の特徴
円周率には終わりがない。
3.141592…と続き、 出てくる数の順番に規則もない。
これらの性質は「無理数」や「超越数」という言葉で表現され、証明されている。壮大だ。
専門的なことは、専門家にまかせるとしよう。
この性質にあやかり、円周率の頭3つの数字から「3月14日を結婚記念日にするひとがいる」と聞いたことがある。永遠の愛を誓うのだと言う。
ここで、この記事のタイトルに戻る。
7月22日は「円周率の日」?、とある。
この「7」「22」とは何か。円周率との関係を書きたい。
円周率に “近い” 数字
7や22と円周率は、一見、なんの関係もないように見える。
試しに円周率の文字列一覧表を用いて調べると、「722」という文字列が円周率の数列の中に登場するのは3,300桁台の話。以降1万桁までに10回登場するが、それを「関係がある」とは言えないだろう。
ところが、「22/7(7分の22)」という数字は、円周率に近い数字として、紀元前2000年頃から円周や面積を求める数として使われてきたようだ。
22/7 = 3.142857(下線部6桁を繰り返す循環小数)
たしかに近い。
古代は「万物を整数と整数の比(=分数)で表現可能」と信じられていたようだから、ここまで近い値があれば広く用いられたことにも納得がいく。
ならば私は、7月22日を「円周率近似値の日」としたい。
けれども、4000年以上の歴史がある数字には、コンピュータを使って求められた最新の円周率よりも、歴史や、探求の心や、そこに人間がいたという事実を強く感じることができる。
突拍子もないように見える数字を求めようとする姿勢に、感動さえする。
「円周率」と「素数」を考える
ここまで書いて気付いたことがある。
私はこれまで、「素数」を考えるにあたり、素数が「永遠に存在する」「永遠に続く」のように、「永遠」という言葉を使ってきた。
しかし、この記事を書いて、「円周率」や「素数」について考える時に連想される「終わりがない」という特徴には、違いがあると感じている。
「素数が永遠に続く」と言う時は、素数と名付けられた数が終わりなく存在する、という意味。対して、
「円周率が永遠に続く」と言う時は、円周率というたった一つの数が終わりなく続く、という意味だ。
ということは、
素数は「無限に存在する」
円周率は「永遠に続く」
のように、「終わりがない」という言葉を使い分けたほうがよいかもしれない、と思った。
まだ、自分にとっての答えが見つかったわけではないが、これからも考え続けたい。
まとめ
・「円周率」とは「円の周りの長さを求めるための数(倍率)」のこと
・円周率に近い値の「22/7」より、7月22日を「円周率近似値の日」としたい
・「無限」と「永遠」の違いについて考える
